 MORFOMETRIA GEOMÉTRICA: CARACTERÍSTICAS GENERALES Y SU APLICACIÓN EN ARQUEOLOGÍA
MORFOMETRIA GEOMÉTRICA: CARACTERÍSTICAS GENERALES Y SU APLICACIÓN EN ARQUEOLOGÍA
Lic. Hernán A. Marani
CONICET – INCUAPA, Facultad de Ciencias Sociales (UNCPBA). Av. Del Valle 5737 (CP 7400) Olavarría.
E-mail: Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
Recibido 26 de agosto 2010. Aceptado 9 de septiembre 2010.
RESUMEN
En este trabajo se presentan las características generales de la Morfometría Geométrica como herramienta para investigar en profundidad los cambios en forma y tamaño de los objetos a fin de evaluar patrones distribucionales, evolutivos, filogenéticos, entre otros. Esta técnica, originalmente desarrollada para el estudio de las formas biológicas, está siendo aplicada en otras disciplinas como la geología, paleontología, medicina, antropología forenses y recientemente se empezó a utilizar en arqueología. Dentro de esta disciplina, la morfometría geométrica está siendo empleada para el estudio de la variabilidad morfológica e historia de vida (e. g., reactivación de instrumentos líticos y la forma y funcionalidad de artefactos óseos). A modo de ejemplo se presentan algunos casos de estudio.
Palabras clave: Morfometría geométrica; Arqueología; Industrias ósea y lítica.
ABSTRACT
In this paper, the general characteristics of Geometric Morphometry are presented as a tool to investigate in depth the changes in shape and size of objects, as a means to assess distributional, evolutionary and phylogenetic patterns, among others.This technique, originally developed for the study of biological forms, is being applied in other disciplines such as geology, paleontology, medicine, forensic anthropology and has recently started to be used in archaeology. Within this discipline geometric morphometrics are being used to study the variability and live history (e.g. reactivation of stone tools and form and functionality of bone artifacts). As an example some case studies are presented.
Keywords: Geometric morphometrics; Archaeology, Bone and stone industry.
CARACTERÍSTICAS GENERALES Y SU APLICACIÓN EN CIENCIAS NATURALES
Este trabajo no pretende hacer un análisis detallado de la Morfometría Geométrica y todas sus técnicas de estudio de las formas, simplemente se busca presentar un panorama general de sus herramientas y su aplicación en diferentes campos de las Ciencias Naturales y la Arqueología.
La morfometría geométrica se desarrolló a finales de los años 80 como una variante a la morfología clásica. Esta técnica revolucionó los estudios morfológicos a partir de cambios en la estimación de tamaño y forma de las estructuras analizadas. A diferencia de la morfometría clásica que estudia dichos cambios a través de análisis multivariados empleando medidas lineales entre puntos morfológicos, la morfometría geométrica, los analiza a partir de desplazamientos en el plano o en el espacio de un conjunto de puntos discretos denominados landmarks (Van der Molen et al. 2007).
Los landmarks son puntos en el espacio en dos o tres dimensiones que se corresponden a la posición de un rasgo en particular de un objeto. Por ejemplo, en el estudio de formas biológicas los landmarks pueden ser definidos sobre estructuras concretas como huellas de inserción muscular, forámenes, suturas óseas, etc. (Figura 1a). En el caso de estudios arqueológicos realizados sobre tecnología lítica u ósea, los landmarks se definirán sobre rasgos particulares del instrumento analizado, siempre que este rasgo se encuentre presente en toda la muestra analizada (Figura 1b). Tal como se mencionó los landmarks deben estar ubicados sobre el mismo rasgo morfológico a lo largo de toda la muestra estudiada, por lo que las estructuras estudiadas deben ser homólogas (similitud en su origen y ubicación dentro de la topografía del espécimen) en cada caso. La homología de los landmarks puede ser puramente operativa o corresponder a estructuras homólogas en sentido evolutivo, dependiendo de cual es el objetivo del estudio. De este modo, los landmarks pueden ser puntos precisos en el objeto que muestren algún significado filogenético, estructural, funcional o de desarrollo (Lele y Richtsmeier 2001; Van der Molen et al. 2007).
Los landmarks pueden ser clasificados en tres tipos diferentes: Bookstein (1991) los llama tipo I, II y III, Lele y Richtsmeier (2001) los denomina tradicionales, confusos y construidos, mientras que Dryden y Mardia (1998) los designan como anatómicos, matemáticos y pseudolandmaks (Van der Molen et al. 2007:8). Los landmarks tipo I, tradicionales o anatómicos (dependiendo del autor que se siga), son punto cuya homología de un individuo a otro se encuentra respaldada por una sólida evidencia o por significado biológico, como por ejemplo, yuxtaposición de tejidos, suturas craneales, inserción de una aleta, etc. (Figura 2a). Los landmarks tipo II, confusos o matemáticos, son puntos cuya homología de un individuo a otro es respaldada únicamente por la geometría. Estos puntos se localizan en lugares de máxima curvatura o en puntos extremos en la morfología (Bookstein 1991) (Figura 2b). Por ultimo los landmarks tipo III, construidos o pseudolandmarks son puntos localizados en cualquier lugar del contorno del objeto o entre dos landmark anatómicos o matemáticos (Lele y Richtsmeier 2001; Dryden y Mardia 1998).Por su parte, Bookstein (1991) define a los landmarks tipo III como los puntos que presentan una coordenada deficiente, por ejemplo cada uno de los extremos de un diámetro mayor o el fondo de una concavidad (Figura 2c) (Van der Molen et al. 2007).
Una vez captada la forma del objeto o espécimen a analizar, la morfometría geométrica estudia la variación morfológica mediante la utilización de cualquiera de los cuatro métodos principales: métodos de superposición, métodos de deformación, métodos basados en distancias lineales y análisis de contornos.
Los métodos de superposición, se basan en superponer una configuración de landmark sobre otra, haciendo que los landmarks homólogos coincidan lo máximo posible de manera tal que pueda obtenerse una mínima medida de distancia entre ambas configuraciones (Rohlf y Marcus 1993). Existen diferentes técnicas de superposición que pueden aplicarse, tales como: Análisis generalizado de Procrustes, Generalized Resistant-fit, Bookstein’s edge matching, pero el desarrollo de las mismas excede los objetivos de este trabajo (para más detalle ver Goodall 1991; Rohlf 1990, 1999; Slice 1996; Bookstein 1982, 1991; entre otros).
El más frecuentemente utilizado es el método de deformación que fue aplicado por primera vez por Sir D’Arcy Thompson (1917), aunque en esta instancia no se había desarrollado aún el fundamento matemático del método. Éste consiste en modificar el área o volumen de la forma de referencia hasta hacerla coincidir con la forma objetivo. Para demostrar las diferencias de forma Thompson (1917) creó las Transformaciones Cartesianas, donde una grilla bidimensional se superpone a la forma consenso de referencia y se deforma hasta que coincide con la segunda forma o forma objetivo. La técnica de deformación más utilizada es la Thin-plate spline que fue propuesta por Bookstein (1989).
El método basado en distancias lineales o análisis de matrices de distancias Euclidianas fue propuesto por Lele y Richtsmeier (2001) y esta basado sobre las relaciones proporcionales entre las distancias de todos los pares de landmarks de dos especimenes o la muestra. Si las proporciones son iguales, entonces los dos ejemplares presentan la misma forma, en cambio, una proporción constante nos informa sobre diferencias de tamaño (Lele y Richtsmeier 2001). El análisis de matrices de distancias euclidianas, se diferencia de las dos técnicas descriptas anteriormente, por el hecho de estar basado en un sistema libre de coordenadas, y porque es un método invariante a la orientación de los objetos bajo estudio (Rohlf y Marcus 1993).
A diferencia de los métodos descriptos en los párrafos anteriores en que los cambios de las formas se basan en la posición relativa de una serie de puntos morfológicos homólogos (los landmarks) el análisis de contornos se emplea cuando lo que se quiere estudiar es la silueta o textura de la superficie donde es difícil establecer puntos homólogos o la estructura a analizar, carece de éstos. En este caso, el contorno completo puede ser considerado como una estructura homóloga (Bookstein 1991). La forma de la estructura es capturada a través de las coordenadas de una secuencia de puntos a lo largo del contorno. Una vez capturada la forma del objeto a estudiar es necesario distinguir entre dos grandes clases de contornos, dado que requieren de diferentes técnicas para su análisis. Por un lado están los contornos que se corresponden con curvas abiertas, es decir, curvas a través de un contorno definido entre dos landmarks (Figura 3a). Este tipo de contorno es analizado por ecuaciones polinómicas simples o aplicando los métodos Parametric Cubic Splines y Bezier, dependiendo de la complejidad de la curva obtenida. Por otro lado, están aquellos contornos definidos por curvas cerradas (Figura 3b). En este caso se utilizan algunas de las variantes del análisis de Fourier, como ser: el análisis de Fourier de un contorno expresado en coordenadas polares, Análisis Elíptico de Fourier o Armónicos de Fourier (para mas detalles sobre estas técnicas se puede consultar Rohlf y Archie 1984; Foote 1989; Rohlf 1990; Temple 1992).
Estos métodos y técnicas de morfometría geométrica han sido empleados en diversos estudios en una amplia gama de disciplinas científicas, que abarcan la biología evolutiva, la geología, la medicina, la antropología forense, entre muchos otros.
En el campo de la biología evolutiva, podemos citar los trabajos de Bacon (2000) que analiza restos fósiles de homínido a través del método de superposición para determinar su asignación filogenético, lo mismo hacen Delson et al. (2001) para restos fósiles de Indonesia pero utilizando una configuración de semilandmarks, el trabajo de Ackermann y Krovitz (2002) en el que estudian los patrones ontogenéticos de los rasgos faciales en el linaje de los homínido, utilizando el análisis de matriz de distancias euclidianas, entre muchos otros. En geología podemos mencionar el trabajo de MacLeod (2002) en el que analiza y clasifica las formas de las partículas sedimentarias a través del análisis de contornos y analiza las formas de los valles fluviales mediante el análisis de contornos de curvas abiertas. Por otra parte, el trabajo de Castillo Jurado (1992) en el que realiza un estudio de la morfología de los lagos de los Pirineos mediante análisis elíptico de Fourier. En medicina se ha utilizado el método de superposición para estudiar los efectos de la exposición fetal al alcohol sobre la forma del corpus callosum y su correlación con problemas neuropsicológicos en hombre adultos (Bookstein et al. 2002a y 2002b). En antropología forense se ha empleado el análisis Elíptico de Fourier sobre el contorno de los senos frontales a los efectos de ser utilizados como método de identificación de personas (Christensen 2005). En un campo más cercano a la arqueología como es la Antropología biológica, la morfometría geométrica se ha empleado como herramienta para evaluar hipótesis sobre el poblamiento temprano del Nuevo Mundo (Gonzáles-José et al. 2008) entre muchas otras aplicaciones.

Figura 1: Distribución de landmarks homólogos a) Landmarks en estructuras biológicas homólogas (Imagen modificada de Cadrin 2010 Figura 9.1:223) y b) Landmarks sobre rasgos característicos de un instrumento lítico (imagen modificada de Franco et al.2005 Figura 2:85)
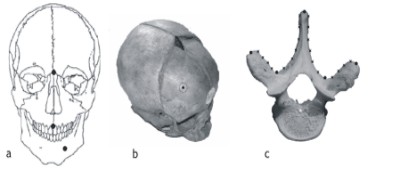
Figura 2: Landmark de Tipo I, tradicional o anatómicos. Ubicados en el foramen mental, en la sutura naso parietal y en la sutura inter-maxilar. b) Landmark de Tipo II, confuso o construido. Ubicado punto de saliencia máxima del lóbulo frontal. c) Landmark de Tipo III, construidos o pseudos-landmark. Los pseudos-landmarks (cruces) están ubicados sobre el contorno de la vértebra, entre dos landmarks anatómicos (imágenes modificadas de Van der Molen et al. 2007; Figuras. 4,5 y 6:9-11)
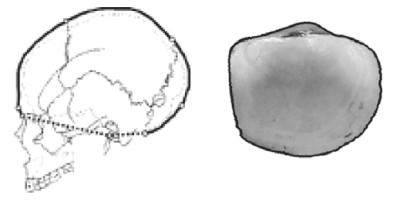
Figura 3: a) Contorno de curva abierta comprendido entre dos Landmarks y b) Contorno de curva cerrada (imagen tomada de Van der Molen et al. 2007 Figura 25: 61)
APLICACIÓN DE LA MORFOMETRÍA GEOMÉTRICA EN ARQUEOLOGÍA
Tradicionalmente en arqueología se han desarrollado sistemas clasificatorios para facilitar el estudio de la variabilidad observada en el registro arqueológico. Muchas de estas clasificaciones, principalmente la clasificación tipológica tradicional desarrollada para los instrumento líticos, se basaron en un reconocimiento intuitivo de patrones morfológicos y funcionales. Dichas clasificaciones se elaboraron utilizando caracteres cualitativos y variables métricas continuas que fueron convertidas en intervalos discretos (Cardillo 2010). Esta discretización de variables continuas, realizadas arbitrariamente, produjo una pérdida de información morfológica e introdujo una mayor variabilidad inter-observador en la identificación de instrumentos dificultando de este modo que algunos análisis líticos puedan ser replicados por otros investigadores (Cardillo 2010).
Una manera de evitar esta pérdida de información y de obtener una aproximación más integral de la variabilidad artefactual es mediante el empleo de estudios morfométricos. Los primeros estudios se desarrollaron en el marco de la morfología clásica donde las variables utilizadas son medidas lineales como la longitud total, el ancho, el espesor y los ángulos (Wynn y Tierson 1990; Crompton y Gowlett 1993; Franco et al. 2005, 2009). Estos estudios estaban interesados en medir la variabilidad dentro de la clase o los cambios morfológicos debido al uso y la reactivación de los artefactos. En años recientes las técnicas morfométricas se centraron en modelos más geométricos (Cardillo 2010).
Uno de los primeros trabajos arqueológicos donde se aplicó la morfometría geométrica fue el de Gero y Mazzullo (1984) donde emplearon el análisis elíptico de Fourier para analizar los desechos líticos de diferentes períodos temporales de Perú. Dentro de esta misma línea, el trabajo de Saragusti et al. (2005) mostró una aplicación potencial de las series de Fourier para explicar la variación de forma de los diferentes artefactos, relacionándolos a la deformación y la simetría. En un trabajo anterior, Saragusti et al. (1998) estudiaron los cambios de la simetría de hachas del Paleolítico inferior mediante la aplicación de formulas matemáticas, demostrando una tendencia temporal hacia artefactos mas simétrico (Cardillo 2010). En argentina los primeros trabajos arqueológicos en los cuales se empleó esta técnica se centraron en el estudio de los cambios de forma de las puntas de proyectil para explorar los cambios en la práctica de subsitencia, cambios estilísticos o cambios funcionales (Cardillo 2005; Castiñeira et al. 2009 y Franco et al. 2009, entre otros), recientemente también se aplico este tipo de análisis a la tecnología ósea, más específicamente al estudio de retocadores de la costa del Golfo San Matías (Marani y Cardillo 2010).
A modo de ejemplo, se desarrollan a continuación, algunos trabajos donde se aplica la morfometría geométrica para el estudio de artefactos líticos y óseos.
CASOS DE ESTUDIO
El primer caso que se presenta es el análisis de la variabilidad métrica y morfológica de pesas líticas recuperadas en la costa del Golfo San Matías. El objetivo planteado por los autores es caracterizar estos artefactos utilizando herramientas de morfometría tradicional y geométrica con el fin de dar cuenta de su variabilidad métrica y morfológica (Scartascini y Cardillo 2009:162). Para este estudio se contó con una muestra de 56 artefactos provenientes de tres localidades arqueológicas de la costa Norte del Golfo San Matías y se empleó el Análisis Elíptico de Fourier dado que este método es el más adecuado para el estudio de contornos cerrados, especialmente en elementos que no presentan landmarks homólogos (Figura 4a).Por otra parte se utilizaron variables métricas, tales como alto de la pieza, ancho, espesor, tamaños de las muescas y el peso, con el fin de establecer relaciones entre éstas y la morfología.
Los resultados del Análisis Elíptico de Fourier determinaron que la forma se describía en detalle con 15 armónicas, los cuales fueron utilizados en el Análisis de componentes principales. Esta prueba estadística dio como resultado que el 90% de la variabilidad total de la muestra era explicada a través de los dos primeros componentes principales. Estos muestran dos agrupaciones discretas donde se ubican por un lado las pesas más alargadas y por el otro las más redondeadas (Figura 4b). Por otra parte se realizó una matriz de correlación entre las variables métricas y los dos primeros componentes principales, mostrando una correlación baja entre el espesor y el primero de los componentes principales. Lo que podría estar indicando un criterio particular para la elección de formas bases para la confección de estas pesas.
Los autores concluyen que las diferencias en tamaños de las pesas líticas podrían estar relacionadas con variaciones en la estrategia de pesca empleada en los distintos sectores de la costa debido a que ésta variable podría afectar la performance de los sistemas de pesca en diferentes ambientes (Scartascini y Cardillo 2009)
El segundo caso es el análisis morfométrico de los cabezales líticos cola de pescado del Uruguay (Castiñeira et al. 2009). En este trabajo los autores analizan 24 puntas de proyectil cola de pescado de colecciones públicas y privadas de la Republica Oriental del Uruguay. El objetivo de este trabajo es analizar si la variabilidad observada se puede atribuir a diferencias estilísticas o a la historia de vida de los artefactos. En este estudio se empleó el método de deformación denominado Thin-plate spline donde la forma fue capturada a través de landmarks y semilandmarks. Los landmarks fueron localizados en los puntos geométricos homólogos, como son el ápice y el punto de máxima curvatura de la base, mientras que los 36 semilandmarks utilizados se distribuyeron a intervalos regulares a través del contorno del instrumento (Figura 5a). Dada la simetría que presenta este tipo de instrumentos los autores tomaron la decisión de analizar la forma de la mitad de la punta de proyectil con el fin de no introducir variabilidad producto de dicha simetría.
Los resultados del análisis de Relative Warps o componentes principales de forma (Figura 5b) señalan que el 55% de la variación morfológica de la muestra se encuentra explicada por el primer componente. Esta variación se manifiesta en el alargamiento y compresión de la forma. El segundo componente, que explica el 20% de la variabilidad muestra cambios localizados, principalmente en la zona del pedúnculo, en el ángulo definido por el hombro y la base del mismo.
En base a los resultados obtenidos, los autores concluyen que la variabilidad de formas y tamaño estarían mayormente relacionadas a la reactivación de los limbos. A mayor reactivación menor tamaño y mayor convexidad de los mismos. Por otra parte, la distribución morfológica no muestra discontinuidades que sugieran la existencia de dos o más grupos estilísticos separados. Esto podría ser interpretado como un gradiente de reactivación entre las formas descartadas luego de una larga vida útil (Castiñeira et al. 2009).
El tercer y último caso se presenta un trabajo donde el método es aplicado para el estudio de la tecnología ósea. En dicho trabajo se analizan retocadores óseos recuperados en la costa del Golfo San Matías provincia de Río Negro (Marani y Cardillo 2010). En este caso los autores analizan 24 retocadores confeccionados de hueso de guanaco con el objetivo de caracterizar la forma de estos instrumentos con el fin de identificar tendencias morfológicas que permitan discriminar diferentes grupos morfo-funcionales. Al igual que en el caso anterior, en este trabajo se aplica el método de deformación Thin-plate spline donde la forma fue capturada a través de landmarks y semilandmarks. En este caso particular la forma fue capturada mediante el empleo de un landmarks que fue ubicado en el extremo activo del retocador (único punto homologo a todos los instrumentos) y 99 semilandmarks que fueron distribuidos a intervalos regulares sobre el contorno de los mismos (Figura 6a). Por otra parte, se emplearon variables métricas tales como el largo máximo, ancho máximo, el ancho y espesor del ápice y el peso, con el fin establecer si estas variables se correlacionan entre sí y con las variables de forma.
Los resultados del análisis de componentes principales indicaron que casi el 64% de la variabilidad morfológica total se encuentra explicada por los dos primero ejes (Figura 6b). El primero de ellos, da cuanta de las variaciones morfológicas de compresión y expansión transversal al eje técnico próximo al extremo activo mientras que el segundo eje da cuenta de cambios localizados en el extremo no activo. A partir de la matriz de correlación se observó que las únicas variables métricas que presentaban una correlación significativa fueron el espesor y el ancho del ápice, por otra parte los dos primeros componentes principales presentaron una correlación significativa con el ancho máximo.
De los resultados que obtuvieron, los autores concluyen que la variabilidad morfológica de los retocadores obedece a diferencias funcionales, en donde se buscó dar una forma determinada al sector activo del instrumento con el fin de obtener extremos mas fino o mas gruesos. La variación morfológica vinculada a estos aspectos funcionales da cuenta de una distribución continua de instrumentos de diferentes espesores, donde en una punta se encuentran los que presentan un extremo activo más grueso y romo y en la otra punta los que son más finos y angulares. Estas variaciones podrían ser vinculadas con observaciones etnográficas que dan cuenta del uso de diferentes tipos de retocadores durante las distintas etapas de regularización de los filos (Marani y Cardillo 2010)
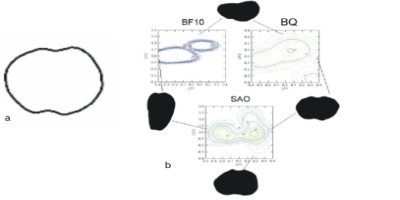
Figura 4: a) Contorno de una pesa lítica (imagen modificada de Scartascini y Cardillo 2009 Figura 2:164). b) Función de densidad de Kernel de los dos primeros componentes (imagen tomada de Scartascini y Cardillo 2009 Figura3:165).
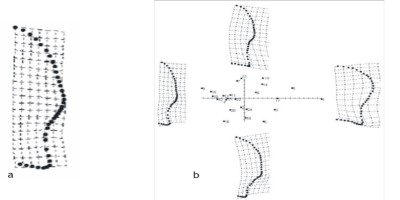
Figura 5: a) Distribución de Landmarks y semilandmarks del lateral de una punta de proyectil Castiñeira et al. 2009 Figura 3:364); b) Gráfico componentes principales (imagen tomada de Castiñeira et al. 2009 Figura 2:363).
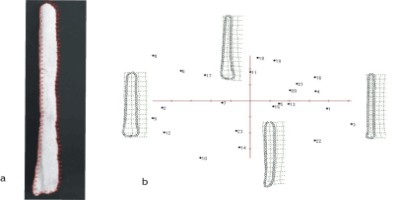
Figura 6: a) Distribución de Landmarks y semilandmarks sobre el contorno de un retocador óseo. b) Gráfico de los dos primeros componentes principales.
CONCLUSIONES
Como lo demuestran los trabajos analizados en la sección anterior, la morfometría geométrica puede ser una herramienta muy poderosa para el estudio de tecnologías líticas y óseas. También podría ser aplicada a la tecnología cerámica para el estudio de piezas completas o para el análisis de las formas de los bordes en piezas fragmentadas. Por otra parte la morfometría geométrica puede ser utilizada como herramienta para generar y testear hipótesis relacionadas a patrones temporales y espaciales en la confección de instrumentos líticos, óseos y/o cerámicos.
AGRADECIMIENTOS
Al Dr. Marcelo Cardillo y la Dra Florencia Borella por la lectura y comentarios que permitieron mejorar el trabajo. Este trabajo fue realizado con Beca Tipo II otorgada al autor por el Consejo Nacional de Investigaciones Científicas y Técnicas, y fue financiado por los proyectos PICT- Agencia 38264 (2007-2009) otorgado a la Dra. Florencia Borella y PIP CONICET N° 112-200801-00756 (2009-2011) otorgado al Dr. Cristian Favier Dubois
BIBLIOGRAFÍA
Ackermann, R. R. y G. E. Krovitz 2002. Common Patterns of Facial Ontogeny in the Hominid Lineage. The Anatomical Record (New Anat.) 269:124-147
Bacon, A. M. 2000. Principal Components Analysis of Distal Humeral Shape in Pliocene to Recent African Hominids: The Contribution of Geometric Morphometrics. American Journal of Physical Anthropology 111(4):479-487
Bookstein F. 1982. Foundation of morphometrics. Annual Review of Ecology and Systematics 13:451- 470.
1989. Principal Warps: Thin-Plate Splines and the Decomposition of Deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence 11: 567-588.
1991. Morphometric tools for landmark data. Geometry and biology. New York, Cambridge University Press.
Bookstein F., P. Sampson, P. Connor y A. Streissguth. 2002a. Midline corpus callosum is a neuroanatomical focus of fetal alcohol damage. The Anatomical Record 269:162-174
Bookstein, F., A. Streissguth, P. Sampson, P. Connor, y H. Barr. 2002b Corpus Callosum Shape and Neuropsychological Deficits in Adult Males with Heavy Fetal Alcohol Exposure. NeuroImage 15: 233–251
Cadrin, S. X. 2010. Stock identification of Marine Populations. En: Ashraf M. T. Elewa, (eds).Morphometrics to Nonmorphometricians. (Lecture Notes in Earth Sciences), pp. 219-232. Springer.
Cardillo M. 2005 Explorando la variación en las morfologías líticas a partir de las técnicas de análisis de contornos. El caso de las puntas de proyectil del holoceno medio-tardío de la Puna de Salta (San Antonio de los Cobres, Argentina). Werken 7: 77:88
2010. Some applications of Geometric Morphometrics to archaeology. En: Ashraf M. T. Elewa, (eds). Morphometrics to Nonmorphometricians. (Lecture Notes in Earth Sciences), pp. 325-341. Springer
Castillo Jurado, M. 1992. Morfometría de los lagos una aplicación a los lago del Pirineo. Tesis doctoral Presentada en el programa de ecología de la Universidad de Barcelona. MS
Castiñeira C, M. Cardillo, J. Charlin, J. C. Fernicola y J. Baeza 2009. Análisis morfométrico de cabezales líticos “cola de pescado” de la Rep Oriental del Uruguay. Arqueometría Latinoamericana, Segundo Congreso Argentino y 1ro Latinoamericano. Vol. 2: 360–366. Buenos Aires. Argentina
Christensen, A. M. 2005. Assessing the Variation in Individual Frontal Sinus Outlines. American Journal of Physical Anthropology 127(3):291-295
Crompton R. H. y J. A. Gowlett 1993. Allometry and multidimensional form in Acheulian Bifaces from Kilombe Kenya. Journal of Human Evolution 25(3):175-199
Delson, E., K. Harvati, D. Reddy, L. F. Marcus, K. Mowbray, G. J. Sawyer, T. Jacob y S. Márquez 2001. The Sambungmacan 3 Homo erectus Calvaria: A Comparative Morphometric and Morphological Analysis. The Anatomical Record 262:380-397
Dryden I. L. y Mardia K. V. 1998. Statistical shape analysis. Chichester, John Wiley & Sons.
Foote M. 1989. Perimeter based Fourier analysis: a new morphometric method applied to the trilobite cranidium.Journal of Palaeontology 63: 880-885.
Franco N. V., M. Cardillo y L. A. Borrero 2005 Una primera aproximación a la variabilidad presente en las puntas de proyectil denominadas “Bird IV”. Werken 6: 81-95
Franco N. V., A. Castro, M. Cardillo y J. Charlin 2009 La importancia de las variables morfológicas, métricas y de microdesgaste para evaluar las diferencias en diseños de puntas de proyectil bifaciales pedunculadas: un ejemplo del sur de Patagonia continental. Magallania 37(1): 99-112
Gero J. y J. Mazzullo (1984) Analysis of artifact shape using Fourier series in closed form. Journal of Field Archaeology 11(3): 315-322
González-José, R., M. C. Bortolini, F. R. Santos, y S. L. Bonatto 2008. The Peopling of America: Craniofacial Shape Variation on a Continental Scale and its Interpretation from an Interdisciplinary View. American Journal of Physical Anthropology 137(2): 175-187
Goodall C. 1991. Procrustes methods in the statistical analysis of shape. Journal of the Royal Statistical Society (53): 285-339.
Lele S. R y J.T. Richtsmeier. 2001. An invariant approach to statistical analysis of shapes. Boca Raton, Florida, Chapman & Hall/CRC.
MacLeod, N. 2002 Geometric morphometrics and geological shape-classification systems. Earth Science Reviews 59: 27-47
Marani, H. A. y M. Cardillo. 2010. Retocadores óseos de Saco Viejo (Río Negro, Argentina).Un enfoque morfogeométrico. En: M. De Nigris, P. M. Fernández, M. Giardina, A. F. Gil, M. A. Gutiérrez, A. Izeta, G. Neme y H. D. Yacobaccio (Eds) Zooarqueología a principios del siglo XXI: aportes teóricos, metodológicos y casos de estudio (En Prensa)
Rohlf F. J. 1990. Fitting Curves to Outlines. En: Rohlf FJ, Bookstein FL (eds.), Proceedings of the Michigan Morphometrics Workshop; Special publication of the University of Michigan Museum of Zoology. Vol 2, pp. 165-177. Ann Arbor, Michigan.
1999. Shape statistics: Procrustes superimpositions and tangent spaces. Journal of Classification 16: 197-223.
Rohlf, F. J. y J. W. Archie. 1984. A comparison of Fourier methods for description of wing shape in mosquitoes (Diptera: Culicidae). Systematic Zoology 33(3):302-317 Rohlf, F. J. y L. F. Marcus. 1993. A revolution in Morphometrics. Trends in Ecology and Evolution 8:129-132.
Saragusti I., I. Sharon, O. Katzenelson y D. Avnir 1998 Quantitative analysis of the symmetry of artifacts: lower Paleolithic handaxes. Journal of Archeological Science 25(8): 817-825
Saragusti I., A. Karasik, I. Sharon y U. Smilansky 2005 Quantitative analysis of shape attributes based on contours and section profiles in artifact analysis. Journal of Archaeological Science 32(6): 841-853
Scartascini F. y M. Cardillo 2009 Explorando la variabilidad métrica y morfológica de las “pesas líticas” recuperadas en el sector norte de la costa del golfo de San Matías. Arqueometría Latinoamericana. 2do. Congreso Argentino y 1ro Latinoamericano. 1: 162–175. Buenos Aires. Argentina
Slice D. E. 1996. Three-dimensional, generalized resistant fit and the comparison of least squares and resistant-fit residuals. En: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE (eds.), Advances in Morphometrics, pp. 179-199. New York: Plenum Press.
Temple J. T. 1992. The progress of quantitative methods in palaeontology. Palaeontology 35: 475-484.
Thompson D. W. 1917. On growth and form. Cambridge University Press.
Van der Molen, S., N. Martínez Abadías y R. González-José. 2007. Introducción a la Morfometría Geométrica. Curso Teórico Práctico. Cuadernillo utilizado en el dictado del Curso de postgrado Introducción a la Morfometría Geométrica.FCNyM-UNLP. MS
Wynn T. y F. Tierson 1990. Regional comparison of the shapes of later Acheulian handaxes. American Anthropologist 92: 73-87